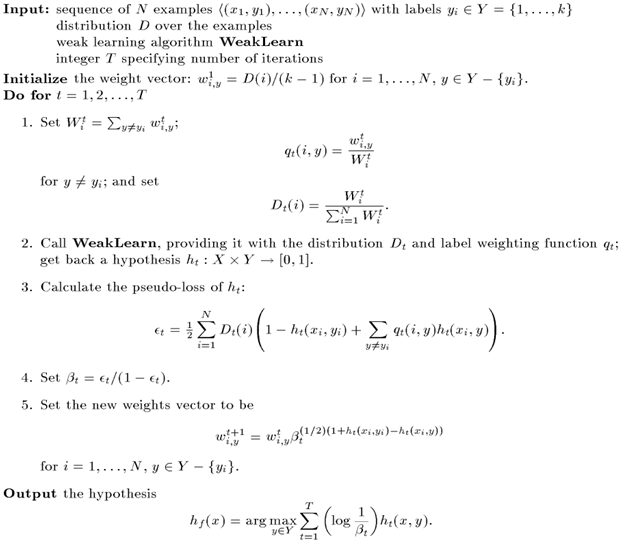Multi Layers Perceptron, PMC (Perceptron Multi-Couches)

Rétropropagation du Gradient

Recuit Simulé

Converges faster than gradient descent

Second order

Radial Basis Functions Neural Networks

You have to chose k

k-means then gradient descent

incremental addition of neurons then exact method

Support Vectors Machine

arbre de décision

based on entropy

k plus proches voisins

[Freund,Schapire, 1995]

Consists in combining a lot of weak classifiers to get a strong one.

ADAptive BOOSTing, [Freund,Schapire, 1996]

The first and standard version is refered as Discrete AdaBoost.

Greedy approach

[Freund,Schapire, 1996]

1. 1997,Freund-Schapire,A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting [Local Copy]

[Friedman,Hastie,Tibshirani, 1998]

1. 1998,Friedman-Hastie-Tibshirani,Additive Logistic Regression - a Statistical View of Boosting [Local Copy]

1. 1998,Schapire-Singer,Improved Boosting Algorithms Using Confidence-rated Predictions.pdf [Local Copy]

[Friedman,Hastie,Tibshirani, 1998]

1. 1998,Friedman-Hastie-Tibshirani,Additive Logistic Regression - a Statistical View of Boosting [Local Copy]

[Friedman,Hastie,Tibshirani, 1998]

1. 1998,Friedman-Hastie-Tibshirani,Additive Logistic Regression - a Statistical View of Boosting [Local Copy]

[Friedman,Hastie,Tibshirani, 1998]

1. 1998,Friedman-Hastie-Tibshirani,Additive Logistic Regression - a Statistical View of Boosting [Local Copy]

AdaBoost is a sequential forward search procedure using the greedy selection strategy to minimize a certain margin on the training set. A crucial heuristic assumption used in such a sequential forward search procedure is the monotonicity (i.e. that addition of a new weak classifier to the current set does not decrease the value of the performance criterion). The premise offered by the sequential procedure in AdaBoost breaks down when this assumption is violated. Floating Search is a sequential feature selection procedure with backtracking, aimed to deal with nonmonotonic criterion functions for feature selection

[Freund,Schapire, 1997]

An extension of AdaBoost to regression problems

1. 1997,Freund-Schapire,A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting [Local Copy]

[Freund,Schapire, 1997]

Basic extension of AdaBoost to multiclass problems. A weak classifier needs to have an error rate less than 1/2, which is stronger than random guessing (1/k) and is often too difficult to obtain.

A weak classifier associates to an example a label in {0,…,k}.

1. 1997,Freund-Schapire,A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting [Local Copy]

[Freund,Schapire, 1997]

Tries to overcome the difficulty of AdaBoost.M1 by extending the communication between the boosting algorithm and the weak learner. The algorithm not only focuses on hard instances, but also on classes which are hard to distinguish.

A weak classifier associates to an example a vector in [0,1]^k, and the pseudo-loss takes also into account weights according to the performance of the weak classifier over the different classes for the same example.

1. 1997,Freund-Schapire,A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting [Local Copy]

[Schapire,Singer, 1998]

1. 1998,Schapire-Singer,Improved Boosting Algorithms Using Confidence-rated Predictions.pdf [Local Copy]

[Schapire,Singer, 1998]

1. 1998,Schapire-Singer,Improved Boosting Algorithms Using Confidence-rated Predictions.pdf [Local Copy]

1. 1998,Friedman-Hastie-Tibshirani,Additive Logistic Regression - a Statistical View of Boosting [Local Copy]

[Schapire,Singer, 1998]

1. 1998,Schapire-Singer,Improved Boosting Algorithms Using Confidence-rated Predictions.pdf [Local Copy]

1. 2006,Sun-Todorovic-Li,Unifying multi-class AdaBoost algorithms with binary base learners under the margin framework [Local Copy]

[Schapire, 1997]

1. 2006,Sun-Todorovic-Li,Unifying multi-class AdaBoost algorithms with binary base learners under the margin framework [Local Copy]

[Guruswami,Sahai, 1999]

1. 2006,Sun-Todorovic-Li,Unifying multi-class AdaBoost algorithms with binary base learners under the margin framework [Local Copy]

[Eibl,Pfeiffer, 2002]

[Eibl,Pfeiffer, 2003]

1. 2003,Eibl-Pfeiffer,Multiclass-Boosting for Weak Classifiers [Local Copy]

[Eibl,Pfeiffer, 2003]

1. 2003,Eibl-Pfeiffer,Multiclass-Boosting for Weak Classifiers [Local Copy]

Stagewise Additive Modeling using a Multi-class Exponential loss function, [Zhu,Rosset,Zou, 2006]

1. 2006,Zhu-Rosset-Zou,Multi-class AdaBoost [Local Copy]

Gentle Adaptive Multiclass Boosting Learning, [Huang,Ertekin,Song, 2005]

1. 2005,Huang-Ertekin-Song,Efficient Multiclass Boosting Classiffication with Active Learning [Local Copy]

Uneven loss function + greedy

Not greedy, exact.

1. [Local Copy]

TOTALly corrective BOOSTing, [Warmuth,Liao,Ratsch, 2006]

1. 2006,Warmuth-Liao-Ratsch,Totally Corrective Boosting Algorithms that Maximize the Margin [Local Copy]

[Li,Abu-Mostafa,Pratap, 2003]

1. [Local Copy]

[Li,Abu-Mostafa,Pratap, 2003]

1. [Local Copy]

(Multiple Instance Learning BOOSting), [Viola,Platt, 2005]

1. 2005,Viola-Platt-Zhang,Multiple Instance Boosting for Object Detection [Local Copy]

Conjugate Gradient BOOSTing, [Li,Abu-Mostafa,Pratap, 2003]

1. [Local Copy]

A cascade of classifiers is a degenerated decision tree, where at each stage a classifier is trained to detect almost all objects of interest, while rejecting a certain fraction of the non-object patterns (eg eliminates 50% of non-object patterns and falsely eliminates 0.1%, then after 20 stages it can be expected a false alarm rate of 0.5^20 and a hit rate of 0.999^20). It enables to focus attention on certain regions and dramatically increases speed.

• MLP (Multi Layers Perceptron)

• RBFNN (Radial Basis Functions Neural Network)

• SVR (Support Vectors Regressor)